|
After a long and sometimes unpleasant campaign, the
US Presidential Election for 2004 took place on the 2nd of November. Polls
opened in New York at 06:00, and closed in Hawaii at 20:00 local time.
The pre-election surveys by various organizations indicated it was a very
close battle, with some giving the edge to President Bush and others to
Senator Kerry. Both campaigns were intensely focused on battleground
states, the must-win states that included Florida, Pennsylvania, Ohio
and a few others with smaller numbers of electoral votes. In the end,
the question came down to which candidate would take Ohio, and it was
Bush, with a small but ultimately undisputed majority (some people still
worry that the new computerized balloting is vulnerable to errors
and even to hacking). Bush also had a
substantial margin of some 2 or 3 million
in the popular vote, and in at noon on 3 November, Kerry called Bush to
congratulate him on having won the election.
The formal prediction
made before the election was that the period defined by the opening to
closing of all polls in the US would show a departure from expectation.
I should note that experience has indicated that political events
typically do not yield notable deviations, but we want to learn what
actually happens in different categories of events, and the methods we
use require that we make a prediction of deviation -- even if we
don't believe that will occur. See note below on Bayesian prediction.
The outcome of the formal analysis is a non-significant negative trend,
with Chisquare of 68129 on 68400 df, which has a corresponding p-value
of 0.768 and Z = -0.732.
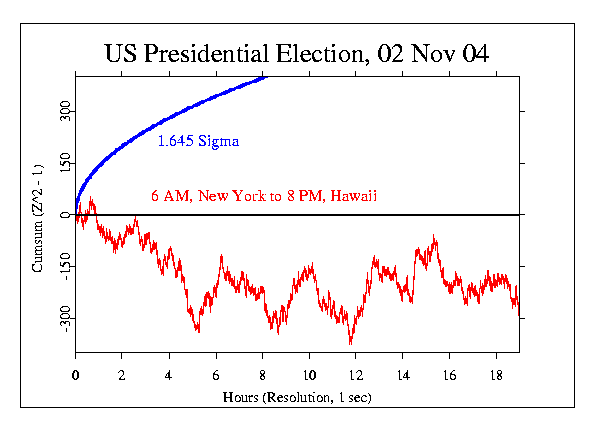
It is interesting to look at a longer period around the formal segment
of data. The next figure shows a few hours before and after, including
the public concession speech by Kerry at 14:00 in Boston. This shows
that except for a few hours at the beginning, the election period
corresponded to a flat trace with no indication of anything but a random
walk.

York Dobyns made a very specific prediction prior to the election that
it would show a "flat" non-significan outcome (much as it in
fact did). He proposes to do, when time allows, a Bayesian analysis
to test this prediction.
|